Homework CFD:SPH

2021年，哈尔滨工程大学《高等水动力学》课程作业：“基于SPH方法的舰船波浪砰击模拟”。

项目	描述
版本：	0.0.2
作者：	左志华（zoziha，zuo.zhihua@qq.com）
网页：	https://zoziha.github.io/SPH-homework/
许可证：	Copyright (c) 2021 左志华

开始

获取仓库

git clone https://github.com/zoziha/SPH-homework.git
cd SPH-homework

使用 mdbook构建文档

mdBook是一个从Markdown文件创建现代在线书籍的实用程序。
你可以通过提供的book.toml文件来构建《高等水动力学作业》。

cd doc && mdbook build

课堂笔记

课堂笔记我做的比较随意，有时候会不自觉地分神，很多内容都没记下来，但是稍微知道老师在讲什么。

第一课

课程目标：1. 水动力学原理；2. 研究前沿。

课程任务：1. 上机操作（8学时）；

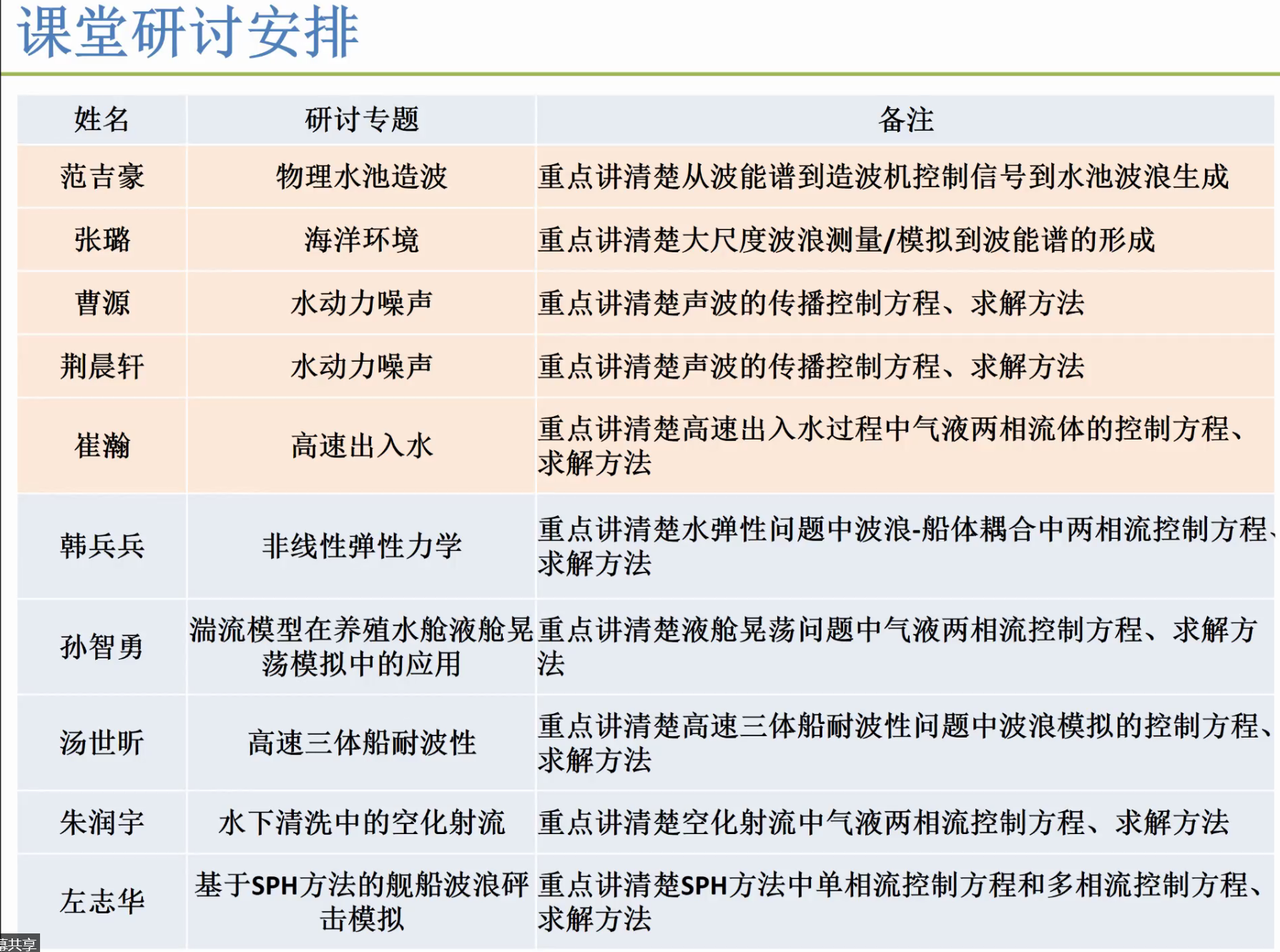
研讨专题

阅读专著、文献，准备相应的PPT，进行汇报。（时间要求：10分钟+5分钟）
周一（1-5号学生）、周三（6-10号学生）（10 左志华）

推荐课本：1. 高等流体力学（上交、科学、哈工大出版社）

流体本构方程

课程要点：1. 流体基本控制方程；2. 本构关系

连续介质假设：

界定区间：[10e-21, 10e-12]

描述流体的宏观物理量：

密度，稳定，速度，压力等。

拉式，欧式（转换）：$\frac{DQ}{Dt}=\frac{\partial Q}{\partial t}+\overrightarrow u\cdot\nabla Q$

物质（随体、全局）导数=局部导数+对流导数。（例子：人的体温）

三大基本定律：质量守恒（物质）、动量守恒（力守恒，瞬态）、能量守恒（过程）

补充方程：1. 本构方程；2. 状态方程。

我的课程题目：船舶砰击的光滑粒子。

浮体，波浪运动。

第二课

博士开题：文献综述

本构方程（减少未知量）；2. 状态方程（增加方程）。（5个方程，12个未知量）

理想流体力学与势流理论不同：无旋方有势。

第二粘性系数（膨胀粘性）：$\lambda$

流体的本构关系反映了应力与变形速率之间的关系。

一般运动=平移+转动+线变形+角变形。

作业要求：1. 研究问题背景；2. 控制方程与假设（数学模型）

CFD：1. FEM、FVM、FDM、ALE；2. SPH、MPS、PFEM。

第三课

湍流模型的提出：考虑涡的随机性，直接计算计算量大、存储量大。

层流，有序；湍流，无序。

直接求解NS方程（直接数值模拟DNS）：与网格量有关，适应粒子法，粒子更自由。

湍流尺度：宏观尺度、积分尺度、泰勒尺度、耗散尺度、分子自由程。

通过先验模型，降低计算量，细节和工程问题需求。

宏观尺度、生成区、惯性区、耗散区。DNS、LES（空间滤波）、RANS（时间平均）。

第四课

雷诺应力模型，大涡模拟(LES)。

涡旋黏性模型(EVE, Eddy viscosity models) 涡黏性假设：流体微团→分子热运动。引入湍流粘性(模型化)系数：Vt 微团脉动项用分子脉动表示，采用混合长度理论，进行推导，也引入了误差，由实验确定混合长度。

0方程使用了混合长度理论和分子热运动。 1方程使用了混合长度理论。 2方程，没有使用混合长度理论。

误差(与精度相似意义)：系统误差。2次近似，包括边界。

湍流模型：布置网格，不能太多，不能太少。只要是正确求解，粒子可以自由地游走。

难点(关注于粒子，相较于网格法十分注重网格，系离散形式)：边界处理，自适应光滑长度，紧支域粒子搜索🔍(算法，降低时间复杂度)

设计模式可借鉴！

第五课

水动力学问题基本假设：一般情况下，将水视为不可压缩流体（密度为常数），忽略环境温度变化（无热能交换）。

数值造波。

溃坝模型和数值造波SPHysics。

自由面追踪。

第六课

使用势流理论求解造波机运动规律，在阻尼区加耗散项（NS方程右边末尾）。

网格法：1. 直接给入口质点赋属性；2. 造波板的运动；3. 源项造波法。

规则波与聚焦波。

势流-粘流耦合方法：避免粘流数值耗散。

课堂研讨

第七课：泰勒展开边界元

四大面向：世界科学前沿、国家重大需求、国家经济主战场、人民健康。

课程作业文档实例

研究背景：舰船砰击的光滑粒子力学仿真

工程研究背景

工程上，一些船舶高速、砰击工况，还主要依赖实验，光滑粒子流体动力学在这方面有一些可探索的优势。

学术研究背景

无网格技术是拉式观点的重要实现，不像网格法，光滑粒子流体动力学理论仍存在不完善的地方。

流体控制方程

摘要：1. 守恒与非守恒式控制方程；2. 积分形式与微分形式的重要注释。

控制方程的通用形式$^{[1]}$

如果用$\phi$表示通用变量，则四个基本控制方程（连续方程、动量方程、能量方程、组分方程）可以表达成以下通用形式：

$$ \frac {\partial (\rho \phi)}{\partial t} + div(\rho u \phi) = div(\Gamma grad \phi) + S $$

其展开形式为：

$$ \frac {\partial (\rho \phi)}{\partial t} + \frac {\partial (\rho u \phi)}{\partial x} + \frac {\partial (\rho v \phi)}{\partial y} + \frac {\partial (\rho w \phi)}{\partial z} = \frac {\partial}{\partial x}(\Gamma \frac{\partial \phi}{\partial x}) + \frac {\partial}{\partial y}(\Gamma \frac{\partial \phi}{\partial y}) + \frac {\partial}{\partial z}(\Gamma \frac{\partial \phi}{\partial z}) + S $$

式中，$\phi$为通用变量，可以代表$u, v, w, T$等求解变量；$\Gamma$为广义扩散系数；$S$为广义源项。
式中各项依次为瞬态项（transient term）、对流项（convective term）、扩散项（diffusive term）和源项（source term）。

表1 通用控制方程中各符号的具体形式

符号	$\phi$	$\Gamma$	$S$
连续方程	$1$	$0$	$0$
动量方程	$u_i$	$\mu$	$-\frac{\partial p}{\partial x_i} + S_i$
能量方程	$T$	$\frac{k}{c}$	$S_T$
组分方程	$c_S$	$D_S \rho$	$S_S$

这样，我们就只需要考虑通用微分方程（1.19）的数值解，编制求解源码，就足以求解不同类型的流体流动及传热问题。
对于不同的$\phi$，只要重复调用该程序，并给定$\Gamma$和$S$的适当表达式以及适当的初始条件和边界条件，便可求解。

非守恒型控制方程$^{[1]}$

由通用控制方程可写成：

$$ \phi \frac {\partial \rho}{\partial t} + \rho \frac {\partial \phi}{\partial t} + \phi \frac {\partial (\rho u)}{\partial x} + \rho u \frac {\partial \phi}{\partial x} + \phi \frac {\partial (\rho v)}{\partial y} + \rho v \frac {\partial \phi}{\partial y} + \phi \frac {\partial (\rho w)}{\partial z} + \rho w \frac {\partial \phi}{\partial z} = div(\Gamma grad \phi) + S $$

根据连续性方程（质量守恒方程，mass conservation equation），

$$ \frac{\partial \rho}{\partial t} + \frac{\partial(\rho u)}{\partial x} + \frac{\partial(\rho v)}{\partial y} + \frac{\partial(\rho w)}{\partial z} = 0 $$

简化为：

$$ \rho (\frac {\partial \phi}{\partial t} + u \frac {\partial \phi}{\partial x} + v \frac {\partial \phi}{\partial y} + w \frac {\partial \phi}{\partial z}) = div(\Gamma grad \phi) + S $$

SPH使用哪一种类型的控制方程是合适的？

积分形式与微分形式的重要注释$^{[2]}$

积分形式与微分形式有着实质性的区别。
积分形式的方程允许在（空间位置）固定的控制体内出现间断。然而，微分形式的控制方程假定流动参数是可微的，从而必须是连续的。
在流动包含真实的间断（如激波）时，这一点变得尤其重要。

参考文献

[1] 王福军. 计算流体动力学分析--CFD软件原理与应用[M]. 清华大学出版社, 北京, 2004.
[2] 约翰 D. 安德森. 计算流体力学基础及其应用[M]. 机械工业出版社, 北京, 2007.

光滑、粒子、NS方程（流体动力学）

光滑(理解为，近似，但它仍应该叫做光滑)

对于网格法，在空间布有网格，即可以照顾到所有所需空间。

而对离散的粒子而言，SPH不是MD，从实际效率上SPH也不能在所需空间内完全布满与真实世界一样密度的真实粒子，所以需要光滑（近似手段），使用伪粒子模拟实际粒子流场特性。

反过来不难理解，尽管我们将流体视为一个个分散的粒子，但流体毕竟是连续充满整个空间的，流体中每个位置参与运算的值都是由周围一组粒子累加起来的。这就是光滑的来由。

以上是从文字描述上来看待问题，以下给出数学定义：

迪利克雷函数 -> 光滑（核）函数。

$$\delta(r) = \left{ \begin{array}{ll} \infty, & if \ r = 0; \ 0, & otherwise. \end{array} \right.$$

满足，$\int{\delta(r)dv}=1$。

任意函数，满足

$$ f(r) =\int_\Omega f(r^{'})\delta(r - r^{'})dr^{'} $$

引入光滑函数，来近似，显然需要满足一些条件让光滑函数保留迪利克雷函数的特质。(SPH习惯用法，核近似用角括弧<>标记)

$$ f(r) \approx <f(r)> =\int_\Omega f(r^{'})W(r - r^{'}, h)dr^{'} $$

不得不提，光滑函数$W$常选用偶函数，需要满足：

正则化条件；
当光滑长度趋于0时，具有迪利克雷函数性质；
紧支性；
偶函数的核函数，具有$h^2$精度或二阶精度。

粒子（亦称为，伪粒子）

从网格法到粒子法，事情并没有那么美好。

与SPH核近似法相关的连续积分表示式可转化为支持域内所有粒子叠加求和的离散化形式。

$$ f(r) \approx <f(r)> =\int_\Omega f(r^{'})W(r - r^{'}, h)dr^{'} \ \approx \sum_{j=1}^N f(r_j)W(r-r_j,h)\Delta V_j \ =\sum_{j=1}^N\frac{m_j}{\rho_j}f(r_j)W(r-r^{'},h) $$

注意到，这里有2处近似。
则粒子$i$处的函数的粒子近似式：

$$ <f(r_i)> \approx \sum_{j=1}^N\frac{m_j}{\rho_j}f(r_j)W_{ij} $$

其中，$W_{ij} = W(r_i-r_j, h)$。

粒子法作为一种无网格法，它也需要面对很多实际问题做出相应的理论和实践解释，这并不比网格法简单。

N-S方程（流体动力学）

3大控制方程 + 补充方程（本构方程，或状态方程），能体会出来，粒子法天然性地满足质量守恒定律（粒子不应该凭空产生，也不该凭空消失）。所以问题就变成了求解N-S方程。

粒子受力分析$^{[1]}$

SPH算法的基本设想，就是将连续的流体想象成一个个相互作用的微粒，这些例子相互影响，共同形成了复杂的流体运动，对于每个单独的流体微粒，依旧遵循最基本的牛顿第二定律。

$$\overrightarrow{F}=m\overrightarrow{a}$$

这是我们分析的基础，在SPH算法里，流体的质量是由流体单元的密度决定的，所以一般用密度代替质量

$$\overrightarrow{F}=\rho\overrightarrow{a}$$

这里$F$的量纲发生了变化，需要注意！
易知：

$$\overrightarrow{F} = \overrightarrow{F}^{external} + \overrightarrow{F}^{pressue} + \overrightarrow{F}^{viscosity}$$

重力

外部力一般是重力。

$$\overrightarrow{F}^{external} = \rho \overrightarrow{g}$$

压差作用力

由流体内部的压力差产生的作用力。

$$\overrightarrow{F}^{pressue} = -\nabla p$$

粘性力

由粒子之间的速度差引起的。

$$\overrightarrow{F}^{viscosity} = \mu\nabla^2\overrightarrow{u}$$

NS方程

联立上式，得

$$\rho \overrightarrow{a} = \rho \overrightarrow{g} -\nabla p + \mu \nabla^2\overrightarrow{u}$$

加速度形式：

$$\overrightarrow{a} = \overrightarrow{g} - \frac{\nabla p}{\rho} + \frac{\mu \nabla^2\overrightarrow{u}}{\rho}$$

实际运算过程中，有时还需要考虑表面张力得影响。

对应SPH中的NS方程形式为：

$$\overrightarrow{a}(r_i) = \overrightarrow{g} - \frac{\nabla p(r_i)}{\rho(r_i)} + \frac{\mu \nabla^2\overrightarrow{u}(r_i)}{\rho(r_i)}$$

SPH推导过程

对于SPH算法来说，基本流程就是这样，根据光滑核函数逐个推出流体中某点的密度，压力，速度相关的累加函数，进而推导出此处的加速度，从而模拟流体的运动趋势。

插曲（标注）：函数空间导数的粒子近似式

$$ \nabla f(r_i) \approx <\nabla f(r_i)> \approx \sum_{j=1}^N\frac{m_j}{\rho_j}f(r_j)\nabla W_{ij} $$

$$ \nabla^2 f(r_i) \approx <\nabla^2 f(r_i)> \approx \sum_{j=1}^N\frac{m_j}{\rho_j}f(r_j)\nabla^2 W_{ij} $$

思考：$\nabla 1 = 0, \nabla^2 1 = 0$。

密度

$$ <\rho(r_i)> \approx \sum_{j=1}^N\frac{m_j}{\rho_j}\rho(r_j)W_{ij} \ = \sum_{j=1}^N m_j W_{ij} $$

压力

$$ <\nabla p(r_i)> \approx \sum_{j=1}^N\frac{m_j}{\rho_j}p(r_j)\nabla W_{ij} $$

粘度

$$ <\mu \nabla^2 \overrightarrow{u}> \approx \mu\sum_{j=1}^N\frac{m_j}{\rho_j}\overrightarrow{u}(r_j)\nabla^2W_{ij} $$

算法实现

SPH算法的基本流程：

初始化粒子，为每个粒子赋上初始位置
计算每个粒子的密度
计算每个粒子的压强
计算每个粒子的加速度
根据临界条件调整加速度
根据加速度计算每个粒子的速度变化
根据速度计算粒子位置的变化
绘制粒子
回到步骤2

参考文献

[1] SPH算法简介: 对我的启蒙[EB/OL].(2018-11-15). (说明：作者原文链接失效，所以仅采用有效参考链接。)

SPH方法的流体控制方程$^{[1]}$

密度的粒子近似法（连续性方程）

粒子法天然满足连续性方程。

密度求和法

适用于广义流体力学问题，体现了SPH近似法的本质。

$$\rho_i = \sum_{j=1}^N{m_jW_{ij}}$$

修正方案（对等式右端正则化）：

$$\rho_i = \frac{\sum_{j=1}^N{m_jW_{ij}}}{\sum_{j=1}^N{(\frac{m_j}{\rho_j})W_{ij}}}$$

连续性密度法

适用于强间断问题的模拟（如爆炸、高速冲击等）。

$$ \frac{d \rho_i}{d t} = \sum_{j=1}^N{m_jv_{ij}^\beta\cdot\frac{\partial W_{ij}}{\partial x_i^\beta}} $$

动量方程的粒子近似

$$ \frac{dv_i^\alpha}{dt} = -\sum_{j=1}^N m_j \frac{p_i+p_j}{\rho_i\rho_j}\frac{\partial W_{ij}}{\partial x_i^\alpha} + \sum_{j=1}^N m_j\frac{\mu_i\epsilon_i^{\alpha\beta} + \mu_j\epsilon_j^{\alpha\beta}}{\rho_i\rho_j}\frac{\partial W_{ij}}{\partial x_i^\beta} $$

其中，

$$ \epsilon_i^{\alpha\beta} = \sum_{j=1}^N\frac{m_j}{\rho_j}v_{ij}^\beta\frac{\partial W_{ij}}{\partial x_i^\alpha} + \sum_{j=1}^N\frac{m_j}{\rho_j}v_{ij}^\alpha\frac{\partial W_{ij}}{\partial x_i^\beta} - (\frac{2}{3}\sum_{j=1}^N\frac{m_j}{\rho_j}\cdot\nabla_iW_{ij})\delta^{\alpha\beta}$$

该方法属于直接法，可模拟不同粘度系数的流体。

[1] G. R. Liu, M. B. Liu. 光滑粒子流体动力学--一种无网格粒子法[M]. 湖南大学出版社, 湖南, 2005.

直接数值模拟(DNS)和粒子搜索

直接数值模拟

网格法避免DNS方法的原因，DNS要求的网格数较大，计算量、存储量大。

采用先验的湍流模型，可以减轻求解NS方程的负担。

让我好奇的是，SPH方法中，很多学者往往采用DNS方法分析和实现NS方程的求解。

不过从理论发展阶段上看，一般是先有较为成熟、健壮的DNS实现，才会考虑一些可能的先验模型方案来加速计算。

关于湍流模型在SPH方法上的应用，还需要进一步的学习考究。

最近相邻粒子搜索法, NNPS

湍流模型是考虑DNS计算所需网格量过大而引入。从减低计算复杂度的角度上，NNPS是SPH法中最耗时的部分，所以我想到介绍NNPS。

在粒子的相互作用中涉及到两种技术：1. 最近相邻粒子搜索法(NNPS)；2. 粒子对的相互作用。

不仅要算的对，还需要算的快，还要存储少！

在《光滑粒子流体动力学--一种无网格方法》中，介绍了三种最近相邻粒子搜索(NNPS)算法：

全配对搜索法；2. 链表搜索法；3. 树形搜索法。

全配对搜索法

简单而直接，每次搜索都遍历所有粒子。显然，它的时间复杂度是$o(N^2)$。它不适宜计算粒子数量庞大的问题，只有在粒子数量较少的情况下才可能被使用。

链表搜索法

当粒子近似的光滑长度为空间常量的情况下，链表搜索法是有效的。在实现链表算法时，在问题域内铺设临时网格。如果临时网格单元内的平均粒子数量足够小，则链表搜索法的时间复杂度是$o(N)$。

树形搜索法

树形搜索法非常适合求解具有可变光滑长度的问题，这种算法通过粒子的位置来构造有序树（二叉树、四叉树、八叉树）。树形搜索算法的时间复杂度是$o(N\lg{N})$。

在实际编程实现中，往往可以采用面向对象方法、递归函数等编程手段实现树形搜索法，经有关资料证明，结合树形搜索法的SPH实现是非常高效和健壮的，尤其是用于求解具有可变光滑长度和粒子数量庞大的问题时。

其它方法

SPlisHPlasH是一个使用C++语言编写的SPH实现。

散列哈希
紧凑哈希（这可能是一项时间复杂度更低的高效算法，且有效支持并行计算，见SPH Tutorial）
...

以上只是针对时间复杂度的说明，考虑空间复杂度，则对应考虑数据存储的空间。

以下是一个知乎上有趣的回答例子：

老师让我把全班60本作业本按封面上的学号排好。

于是我灵活运用了快速排序的知识，从本堆中随便抽出一本，把学号比它小的本子放在左边，学号比它大的本子放在右边，再从左边这一堆挑出一本……

如此一来我的排本子的时间复杂度就从普通人用的插入排序的$o(N^2)$变成了$o(N\lg{N})$。周围的同学投来好奇的目光，我洋洋自得，心想学过算法的我就是不一样。

快速排序效率果然很高，不一会儿，

我的桌子就放不下了_(:з」∠)_

(评论：忽略系数和空间复杂度的后果。)

粒子搜索实践：四叉树

构建树形结构；
树形节点查询。

总结

粒子数量巨大的时候，如何处理效率问题（计算效率、数据存储和交互）？应该还是从原理上来处理：光滑粒子。

参考文献

[1] CFD基础理论02：粒子法基本概念
[2] 你在生活中用过最高级的算法知识是什么？
[3] 【流体力学】加和不加湍流模型在NS方程上的体现
[4] 【笔记】SPH流体模拟基础
[5] G. R. Liu, M. B. Liu. 光滑粒子流体动力学--一种无网格粒子法[M]. 湖南大学出版社, 湖南, 2005.

有限粒子法

光滑粒子的发展至今仍存在一定的数值缺陷，其中在粒子缺失较明显的模型边界或者物理量变换较大的非连续性界面附近表现出的核估计精度不足尤为显著。

研究发现，可以通过提高核函数的一致性提高边界区域的计算精度。

Liu等在SPH的基础上通过重构核函数提出了再生核质点法(RK-PM)；
Chen等以泰勒级数展开为基础提出了一种对SPH估计式进行正则化的方法，即修正光滑粒子法(CSPM)，并得到了成功应用；
Liu等基于泰勒级数展开提出了有限粒子法(FPM)。

优点：相比于传统的SPH方法，FPM在核函数的选取上较宽松，边界区域计算精度高，高阶拓展性强。相比于CSPM，FPM可以同时估计核函数及其导数值，一定程度上降低了CSPM中缔结导数用于高阶导数计算而产生的累积误差。

缺点：在处理不连续问题时，若与连续体内部处理方法一致，算法的准确性会大大降低；求解线性方程组一定程度上增加了计算复杂度，计算时间较长；系数矩阵是否奇异不可控，影响计算稳定性。因而使用FPM方法时需对界面进行更精细的处理。

——摘录至《一种考虑界面不连续的改进的有限粒子法》

边界处理和多相模拟

题外话：因为最近导师交给我一个小工程做，这次的内容可能不算丰富。原本想展示一些SPHysics软件的运行结果，比较生动形象。

本周课程讲到的是数值造波的一些技术：大体的思路是采用势流理论的解析解，赋值给粘流造波数值计算。

在SPH方法中，造波就意味着离不开边界处理，比如造波机就是流体求解域的边界。课程老师希望我尝试介绍一下现在SPH法中的一些多相模拟技术。

边界处理

由于SPH方法使用粒子的离散形式，在边界处，粒子近似将出现紧支域被边界截断的情况。如下图：
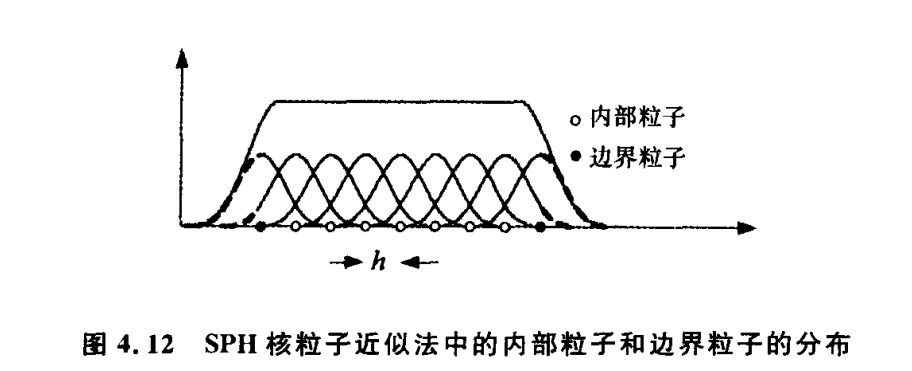
粒子法的边界问题

三种典型边界条件

壁面边界（至少满足不可穿透边界条件）：自由滑移边界、无滑移边界；
自由液面边界；
流入流出边界。

壁面边界的处理一直是SPH方法发展过程中需要重点解决的问题。欧洲光滑粒子研究兴趣共同体（SPHERIC）将固壁边界的处理列为几大挑战性问题之一。

SPH边界处理方法

动态边界；
排斥力边界；
周期开放边界；
等等。

动态边界

边界粒子被要求满足与流体粒子相同的公式，比如连续性方程、动量方程、能量方程和状态方程。
但是它们不需要随着动量方程时间步移动，它们应该保持其边界预设的运动状态。

排斥力边界

排斥力边界被设计，确保流体粒子不能穿透固体边界。

周期开放边界

多相模拟

自由液面流动

2009年，Colagrossi等人从理论的角度证明了弱可压SPH方法在自由液面处能自动满足自由液面边界条件，且自由液面处核函数的截断不影响自由液面模拟的精度。

流固耦合动力学

流固耦合动力学问题中最主要的难点在于刚体或弹性体运动与流场运动的耦合。 SPH方法在模拟流固耦合问题时有两类方法，分别是：
（1）采用纯粒子法对流场和固体结构进行统一建模；
（2）SPH方法与其它数值方法（如有限元）耦合计算。

SPH方法在模拟剧烈流固耦合问题中已经取得了很大进步，但是考虑结果表明边界层效应的流固耦合SPH方法较为少见。

采取自适应粒子细化、聚合技术，在提高局部计算精度的基础上，减小总计算量，为较大规模船舶与海洋工程水动力学问题的数值计算提供技术支撑。

多相流

SPH方法基于拉格朗日观点，在模拟多相流问题时无需特意追踪水气界面，而且模拟多相流界面的破碎和融合时，无需额外的人工干预。

在物体入水研究中，空气的卷入对入水过程的运动和载荷特性有较大的影响。而且，在多相流SPH方法中，受空气粒子密度较小的影响，时间步会比单相流（水）SPH方法中小很多。

比如，时间步长满足${^{[3]}}$，

$$\Delta{t} \le \lambda\frac{\rm{particle\ diameter}}{\max{v_i}}$$

比粒子速度大得多；
根据稳定性、精度需求尽量小；
CFL（Courant–Friedrichs–Lewy）条件是上界；
推荐尺度选择：$\lambda \approx 0.4$；
在模拟过程中自适应时间步。

解决方案

粒子自适应细化、聚合技术。采取自适应粒子细化、聚合技术，在提高局部计算精度的基础上，减小总计算量，为较大规模船舶与海洋工程水动力学问题的数值计算提供技术支撑。

参考文献

[1] 孙鹏楠. 物体与自由液面耦合作用的光滑粒子流体动力学方法研究.
[2] SPHysics.
[3] Introduction, Foundations, Neighborhood Search. Page42

第四次作业：从傅里叶计算地球温度说起（题目待定）

在这次作业的时候，网页引擎已经被换成mdbook来构建了。

老师让我们讲一讲关于2021年诺贝尔物理学奖获得者的内容，因为气象与流体力学是有着紧密联系的。

这次的仓库更改，发现GitHub不适合存储pptx等office文档，还是以pdf为优。

概要

我之前在B站看到以为女生出的一个视频，讲的就是从傅里叶到温室效应，刚好与我这次要讲的、感兴趣的是一致的，而且由于各种不可抗因素，我没有很多时间来准备这次课上汇报，我明天早上汇报，我现在（晚上8点）才开始准备汇报内容。

温室效应

温室效应（英语：Greenhouse effect）是指行星的大气层因为吸收辐射能量，使得行星表面升温的效应。由于温室效应，行星表面温度会比没有大气层时的温度要高$^{[1][2]}$。以往认为其机制类似温室使其中气温上升的机制，故名为“温室效应”。不少研究指出，人为因素使地球上的温室效应异常加剧，而造成全球暖化的效应。

太阳光谱能量

温室效应

傅里叶变换、热传导方程与温室效应

热传导方程的求解

$$\frac{\partial{u}}{\partial{t}}=k\frac{\partial^2{u}}{\partial{x^2}}$$

其中，u是温度，t是时间，x是空间坐标，其它是比例系数。

任意一个热传导问题，都由三部分组成：控制方程、边界条件（空间）、初始条件（时间）。

傅里叶：

对简单和原始问题的考虑是发现自然现象法则的最明确的方法之一，并且正如我们看到的，在科学史上，所有理论都是根据这种方法形成的。

一维问题，直接分离变量；二维问题，令$\partial{u}/\partial{t}=0$，利用分离变量法求解，由于三角函数的正交性。

由此，傅里叶得出傅里叶级数。

傅里叶对地球温度的求解

背景：1901年，诺奖首次颁发；1906年，人类发现地核；1936年，人类发现地核有内核、外核。

1827回忆录中记录了傅里叶的思考：是什么控制了地球的温度？为什么黑夜的一面不会冰冷刺骨？

他考虑了三种热源：太阳、地球的原始热量、与外空间的热交换。

他注意到每深40米，温度会增加一度。这种地热形成与地球诞生之日，并在之后的日子逐渐冷却。傅里叶认为地热对地表温度影响很小。（各地观测到的地热基本相同，且不随时间显著变化）

傅里叶认为外太空温度为-70°C（实际上，外太空接近决定零度，则被认为是宇宙大爆炸留下的残余温度），以此为边界条件。

但这不影响傅里叶的分析，并计算了太阳照射时的理论温度分布，计算显示，被照射处与未被照射处温差巨大，远远大于实际的日温度波动，无疑与实际不符。

傅里叶考虑到，地球表面的气体可能影响了温度分布，他考虑了一种玻璃罩子模型，几层玻璃盖子依次嵌套，大气有这种类似“玻璃罩”作用，傅里叶大概是第一个想到将大气的不均匀吸热视为对地面温度产生影响的人。

备注：地球“温室”不是玻璃“温室”。

二氧化碳登场

30多年后，爱尔兰物理学家丁铎尔通过实验确定了大气中哪些气体具有温室效应。丁铎尔曾明确指出，他测量温室气体的目的是为了解释大气的温室效应及其对地球气候的影响。丁铎尔发现大气的温室效应只是几种含量很少的由三原子组成的分子贡献的，也就是CO2和H2O等，而大气的主要成分氮气和氧气并没有温室效应。

1896年化学家Svante August Arrhenius（1903年诺贝尔化学奖得主）发现二氧化碳和水的红外线吸收效应，他证明了傅里叶的假设，并进行了实验，他在论文中预测了今天温室效应的发生。他在19世纪末用辐射平衡模型得出结论，如果大气二氧化碳水平减半，那么将进入一个冰河时代。反之，如果二氧化碳浓度翻倍，那么温度将会上升5-6摄氏度，这与现代的估计值（2~4.5摄氏度）已经相当接近了。

备注：可见光被地表和海洋吸收，并转化为红外光。

对温室气体的正确和全面的理解是在分子结构物理学和量子力学建立了之后才有的。

当气候科学进入20世纪之后，它的发展极大地得益于物理学，尤其是物理学中关于分子结构的认识以及量子力学的发展极大地促进了人们对气体分子吸收谱(分子光谱)的理解。这些物理学理论告诉我们，一种气体分子的吸收谱是由其分子结构决定的(如CO2和水汽的分子结构决定了它只吸收和放出红外波段的电磁波)，吸收谱中的每一根吸收线实际上是该分子在两个振动态之间的能量差，是量子选择性吸收的结果。在此基础上，温室气体的吸收谱也在实验室得到了广泛和准确的测量。

一个对气候学发展具有重要贡献的是天文学领域辐射传输理论的发展和完善。在20世纪初期，天文学家和天体物理学家出于对恒星结构以及恒星内部能量的径向辐射和对流的研究兴趣，建立了辐射传输的基本理论，这方面的代表性工作是施瓦氏在1906年发表的论文。

实际上，水蒸气是最强大的温室气体，我们无法控制大气中水蒸气的浓度，然而可以控制二氧化碳的浓度。

Manabe和Wetherald：把全球变暖的问题推向了现代

Manabe和Wetherald设计了更为真实的辐射传输模式，并充分考虑了水汽的吸收谱以及水汽的反馈作用。他们最为重要的贡献是考虑了大气的对流运动，并清楚地解释了在地面和大气层顶的辐射平衡问题。正因为如此，人们才认为是Manabe和Wetherald的工作真正把全球变暖的问题推向了现代。半个世纪过去了，他们的论文仍然是我们认识全球变暖最基础的参考文献。

在1960年代，计算机的计算能力还不是很强大。为了简化计算，Manabe将模型缩小到一维——一个垂直的柱子，并且他还忽略了氧气和氮气对地表温度的影响。最后得出的结果显示，当二氧化碳水平翻倍时，全球温度升高了2°C以上，这个结果现在来看还是非常准确的。

1967年的6月，气候模拟学者真锅淑郎（Syukuro Manabe）和理查德·韦瑟尔德（Richard Wetherald）在《大气科学杂志》上发表了很可能是最伟大的一篇气候科学论文《给定相对湿度分布的大气热平衡》。两位作者基本终结了关于二氧化碳是否导致全球变暖的辩论，并建立了一个数学上可靠并首次产生物理真实结果的气候模式。他们用辐射强迫——一种人类或自然变化导致地球能量平衡变化的量值——来理解气候变化的历史原因，这份工作衍生出现代气候模式的发展。从范吉豪同学的汇报中，可以看到，里面有着专业性、晦涩难懂的控制方程和气象模式，很强。

除此之外，还有很多相关的研究在为现代气候模型建立理论支撑。

理论计算 -> 试验 -> 仿真（理论计算）。

像真锅淑郎本人描述，他作为一名应用物理学家，获得诺贝尔奖是惊讶的，奖项背后的实质是对人类和人类家园——地球的关怀。

目前，全球气候变暖已不是单纯的学术问题，而是早已成为国际社会和各国政府所关心的政治问题。这相当于是我个人对全球变暖的科学基础和许多概念、科学历史进行了简单的了解。

心得

很多研究，都是有非常连贯的历史传承，其中参与的每一个人都是可敬的，他们为人类对大自然规律的认识起到了引导性作用。各种奖对我们来说是遥远的，国际研究热点还是可以接触的，脚踏实地，仰望星空，数风流人物，还看今朝。

在人民文学出版社的鲁迅全集第十二卷有这样的一封信表面，鲁迅先生关于诺贝尔奖，表明还是照旧的没有名誉而穷之为好吧。

我还年轻，还是比较“爱慕虚荣”，我本人是fortran-lang组织的开发者之一，今天讲到的傅里叶变换，我现在就是fortran-lang/fftpack（快速傅里叶变换包）的打杂的。

欢迎大家加入fortran-lang社区，我们正在重建fortran社区，这里集结了全球接触开源最厉害的fortran开发者们。

参考资料

维基百科：温室效应. (https://zh.wikipedia.org/wiki/%E6%B8%A9%E5%AE%A4%E6%95%88%E5%BA%94)
傅里叶变换、热传导方程与温室效应（解说+字幕！）(https://www.bilibili.com/video/BV1NJ411b7EZ?spm_id_from=333.999.0.0)
Annex II Glossary. Intergovernmental Panel on Climate Change. [2016-08-20].
A concise description of the greenhouse effect is given in the Intergovernmental Panel on Climate Change Fourth Assessment Report, "What is the Greenhouse Effect?" FAQ 1.3 - AR4 WGI Chapter 1: Historical Overview of Climate Change Science, IIPCC Fourth Assessment Report, Chapter 1, page 115: "To balance the absorbed incoming [solar] energy, the Earth must, on average, radiate the same amount of energy back to space. Because the Earth is much colder than the Sun, it radiates at much longer wavelengths, primarily in the infrared part of the spectrum (see Figure 1). Much of this thermal radiation emitted by the land and ocean is absorbed by the atmosphere, including clouds, and reradiated back to Earth. This is called the greenhouse effect." Stephen H. Schneider, in Geosphere-biosphere Interactions and Climate, Lennart O. Bengtsson and Claus U. Hammer, eds., Cambridge University Press, 2001, ISBN 0-521-78238-4, pp. 90-91. E. Claussen, V. A. Cochran, and D. P. Davis, Climate Change: Science, Strategies, & Solutions, University of Michigan, 2001. p. 373. A. Allaby and M. Allaby, A Dictionary of Earth Sciences, Oxford University Press, 1999, ISBN 0-19-280079-5, p. 244.
傅里叶. 热的理论分析. 1822.
百度百科：诺贝尔奖. (https://baike.baidu.com/item/%E8%AF%BA%E8%B4%9D%E5%B0%94%E5%A5%96/187878)
知乎：地球为何有一颗炽热的心？地核最终会冷却吗？(https://www.zhihu.com/question/21028551)
真锅淑郎获得诺贝尔物理学奖，还得从200年前傅里叶计算地球温度说起. (https://xw.qq.com/cmsid/20211006A0707H00?f=newdc)
百度百科：阿伦利乌斯. (https://baike.baidu.com/item/%E9%98%BF%E4%BC%A6%E5%88%A9%E4%B9%8C%E6%96%AF/15735736)
“气候变暖”，科学家这样解释。和你想的一样吗？(http://www.tanjiaoyi.com/article-14635-8.html)
2021年诺贝尔物理学奖成果解读(附获奖者论文链接). (https://www.aisoutu.com/a/730677)
【谈鲁迅合集】3300W播放！鲁迅：愿中国青年都摆脱冷气，只是向上走。(https://www.bilibili.com/video/BV14f4y1E79N?spm_id_from=333.999.0.0)
fortran-lang组织

高等水动力学作业

使用mdbook构建文档

使用 mdbook构建文档